DAVID GILES | APPLICATIONS ENGINEER – ORDNANCE
Ordnance products are typically considered one-shot devices. When activated, the action is irreversible. Either a permanent deformation of a material occurs, such as a shear pin breaking which releases a firing pin to move, or a chemical reaction occurs, such as initiation of an energetic load within a percussion primer. The device
cannot go back to its initial state.
A light switch can be tested many times to ensure it will work. However, if by testing a component, you destroy the component, how can one know that the device will work? This question is especially critical for pyrotechnic devices that are used in mission critical systems as they must work because millions of dollars of hardware or human lives are at stake. By examining or testing other components, the reliability of an unfired component can be ascertained. To establish reliability, one can turn to everyone’s second favorite subject – statistics.
A subset of statistics that can be computed based on standard deviation is reliability. Standard deviation is a measurement of the amount of variation of a characteristic. Reliability is defined as the ability of a component or system to function. This is usually defined by a value close to 1 and sometimes identified by the number of nines. For example, a 0.99995 reliability is referred to as “four nines five reliable”. An element of reliability that is sometimes overlooked is confidence level. Confidence level is the probability that the reliability is accurate, usually stated as a percentage. Confidence for reliability calculations is usually assessed at 50% or 95% depending on applications.
Reliability and confidence level are implemented for ordnance devices as part of the greater system reliability. Data is used to predict margin of a design and robustness of nominal conditions. Individual analyses for components flow into a higher-level calculation for the system. System level reliability predictions use component data from many devices. Depending on redundancy and linkages, the system is broken down into a block diagram for simpler calculation. Components are considered in series or in parallel to determine the fault tolerance, or reliability, of the system. Even within one component, multiple characteristics can be examined for reliability.
Characteristics Overview
Depending on the application, many different characteristics can be examined for their contributions to reliability. A select few are examined here.
“All-fire” is a characteristic often examined for reliability for ordnance devices. Due to use in safety critical applications, the ensured firing of an ordnance device is imperative. To quantify the “sure” or “all” fire of a given device, firing tests are often performed based on the input signal. Input signals to transfer lines, such as Shielded Mild Detonating Cord (SMDC) or Flexible Confined Detonating Cord (FCDC), are flyer plates of the donor end tips. The end tip to end tip orientation is varied for distance, angle, or offset. Test conditions are at extremes well beyond the design so the failure point can be found. Input signals to percussion primer devices involve a firing pin, often with an input gas pulse. By varying the impact energy of the firing pin via dropping a weight from various points well below the design energy, the failure point can be found. Another example is electro explosive devices (EEDs) which use an electrical signal to initiate. The electrical voltage can be varied to find the failure point.
Besides “all-fire”, the lack of function or “no-fire” can also be assessed via similar methods. This is often used to ensure safety during handling and installation for personnel. Ordnance devices need to function when commanded and not function inadvertently due to the safety risks such as fire or injury often associated with explosives.
Testing for ordnance devices can be destructive and retests are not feasible for the same device. To obtain data, multiple parts must be tested. A nuance to the failure point is that due to tolerances and small variations between each device, the failure point may be slightly different for multiple parts. For an identical input stimulus, a threshold exists where some parts may function, and some may not.
This is called the “crossover” region and the middle of this characteristic is the 50/50 point, or “mean”. The width of the range, sometimes called sigma, is the deviation and is used to determine the reliability of the device. The farther away from the mean, the more certain of successful function or, in the reverse, non-function.
Methodologies
Different methods have been developed to determine the 50/50 point and associated sigma. Before any testing should occur, clear expectations and criteria for what constitutes a passing result and its contrary need to be established. There are six main methods that PacSci EMC uses for reliability analysis, although others do exist.
BINOMIAL
If a binomial distribution is assumed, testing can be performed at the nominal condition, far away from the failure point. With each successful test, determination of the 50/50 point and sigma is distanced from the nominal condition. A positive result moves the nominal down the distribution curve, away from the crossover region.
Calculation of the reliability, when 0 failures are allowable, is given by the following formula:
Rln = 1 -CL
Where Rl is the reliability level, CL is the confidence level, and n is the number of firings. This type of testing requires a significant amount of testing. For example, to obtain a 0.999 reliability at 95% confidence, 2995 successful tests would be required.
Normally a binomial distribution is assumed but other distributions can be used based on the physics of the device. Exploration of other distributions is left as an exercise for the reader to research further.
BRUCETON
Developed in the late 1940s, the Bruceton method is a systematic way of finding the reliability of a system. It requires two initial inputs, a guess of the mean 50/50 point and a step size. For most circumstances, the best input for step size is one standard deviation of the distribution curve. Other step sizes can be used but will require more tests to get to the same conclusion. The same goes for the guess of the mean as a closer guess will need less test assets. Once the initial parameters are established, tests are performed.

If a test is a success, the stimulus is stepped up by one step size and the test is repeated. The stimulus continues to go up by 1 step as long as successes continue. Once the alternate result is achieved, the stimulus is then decreased until the opposite result occurs. This up and down behavior is continued until a significant number of tests have occurred. Based on the desired confidence level, the number of successes and failures are then put through an algorithm to calculate the reliability.
Bruceton testing is most successful and efficient when applied to devices that have a large population of data and parameters that are well established. PacSci EMC uses the Bruceton method for percussion primer initiation testing by adjusting the input stimulus of a ball, dropping it at different heights. The sample size is set at 50 units.
LANGLIE
An upgrade to the Bruceton method was developed in the 1970s, the Langlie method. This test method is similar to the up-down method of Bruceton except that it is less dependent on the initial step size. The initial parameters are a lower and upper bound that fully encompasses the cross-over range.
During testing, the stimulus is set as an average of the last results, with the delta in stimulus depending on a success or failure of the latest tests. The advantage of this is most apparent if the variance of either the mean or sigma is significant compared to previous sets of hardware. In this case, the Langlie algorithm will hone in on the new crossover region much more quickly than the Bruceton.
NEYER
Bruceton and Langlie use simple algorithms to calculate the next value. With the advent of computers, large calculations could be performed. Also called the “D-Optimal” algorithm, the Neyer method requires an upper and lower guess for the mean and a guess for sigma as starting parameters. Then the algorithm uses matrix math and the determinant to find the optimal step and stimulus for the next test as well as calculate the reliability values. The advantage is that the information from all previous tests can be utilized. By leveraging the test history, the amount of testing required to achieve the fidelity needed for reliability and confidence level results is reduced compared to other methods. The Neyer method also hones in on a variance in sigma or mean compared to legacy data even quicker than the Langlie method. We use the Neyer method for many flight termination component studies, with samples sizes as low as 20.
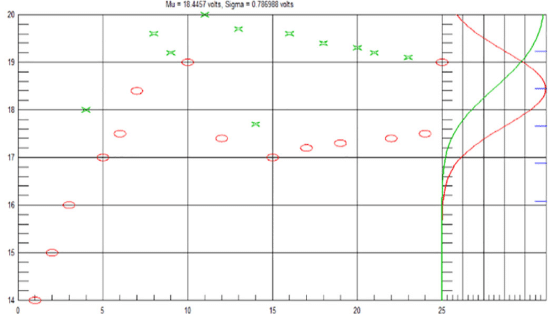
Because the Neyer method is adaptive, the minimum step capability of the test setup can greatly influence the results. The smaller the minimum step compared to the standard deviation of the crossover, the more accurate the results can get. If the minimum step of the test is too large, no crossover may occur, and the calculation will not gain any efficiencies from other methods.
STRESS-STRENGTH
When analyzing a device and its full operation, the above methods are sometimes insufficient as multiple variables and variations can affect the device. Additionally, tolerances of the target surface can affect the system reliability. For these cases, sometimes the Stress-Strength method can be employed.
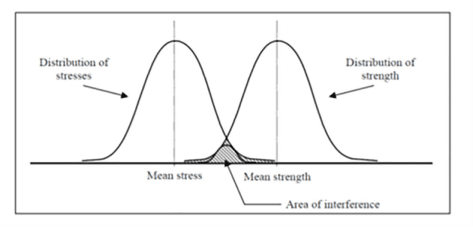
In this model, strength is the amount of energy or output available for the component to function. The amount of output available is defined by a probability density function. Conversely, the target or acceptor stress is defined as how much input energy or stress is needed to break or initiate. This is also defined as a probability function. The two distributions will overlap at some point. This interference area is equal to the unreliability of the interaction. The term “interference” is used to designate an occurrence where stress exceeds strength, so reliability is the probability of no interference.
Margin testing is used at PacSci EMC to demonstrate reliability. Parts may be underloaded to 80% or less and tested. Extra thick witness coupons are demonstrated to be severed with a nominal ordnance device. If the distribution of the energy for part to part variation can be characterized for the input and outputs, a reliability value can be calculated. In the case of no sigma data, typically a value may be assumed as 0.05 to 0.15 of the mean
Standards
Certain government or industry standards have established criteria for acceptability and reliability. These blend historical data and stress-strength modeling to provide a firm requirement for acceptability. Although not directly a statistical method, the basis of these specifications requires a minimum amount of testing or data to prove out device margin and function.
One area where this is used is detonation transfer over an air gap. For instance, two key standards, RCC-319 for flight termination systems and AIAA S-113 for commercial space operations, use multiple series of five tests at margin conditions based on the device tolerances to prove out a reliable transfer.
Conclusion
Although repeated testing of ordnance devices is not possible, the reliability of these types of devices can still be established. Using test data, margin data, manufacturing tolerances, and failure points, different methodologies have been established using statistical methods to construct reliability analyses. These individual reliabilities can then be flowed into system level requirements to allow for full mission assurance.
Reliability and confidence levels are just numbers. The inherent design capabilities are what they are. Depending on system redundancy, resources, assets, and budgets, a low reliability number based on limited data can be improved with additional testing and analyses. Low reliability can also be improved by tightening of manufacturing tolerances or reworking designs for additional robustness where reliability concerns have been identified.
PacSci EMC has a long heritage of high reliability devices used for critical applications. Robust processes and robust testing methods give confidence for key characteristics in the repeatability and the variation to prove out reliable function when commanded and safety when needed.